Background

In Minecraft, the Eye of Ender will fly in a straight line toward the stronghold when used.

Theoretically, using two Eyes of Ender from different starting points will create two intersecting straight lines, and the intersection point of these lines represents the location of the stronghold.

Koala has recorded two different coordinates for each Eye of Ender as it flies. Your task is to determine the coordinates of the stronghold.

Formally, in a 2D Cartesian coordinate system, you are given two distinct points $A_1(x_1, y_1), A_2(x_2, y_2)$ on line $l_1$ and two distinct points $B_1(x_3, y_3), B_2(x_4, y_4)$ on line $l_2$. It is guaranteed that $l_1$ and $l_2$ are not parallel. Your task is to find the coordinates of their intersection point.

Problem Statement

In a 2D Cartesian coordinate system, you are given four coordinates, representing two distinct points $A_1(x_1, y_1), A_2(x_2, y_2)$ on line $l_1$, and two distinct points $B_1(x_3, y_3), B_2(x_4, y_4)$ on line $l_2$.

It is guaranteed that $l_1$ and $l_2$ are not parallel. Your task is to determine the coordinates of the intersection point of $l_1$ and $l_2$.

Input Format

• The first line contains four integers, representing the coordinates of two distinct points $A_1(x_1, y_1)$ and $A_2(x_2, y_2)$ on line $l_1$.
• The second line contains four integers, representing the coordinates of two distinct points $B_1(x_3, y_3)$ and $B_2(x_4, y_4)$ on line $l_2$.

All input coordinates and the output coordinates are guaranteed to be integers, and the absolute values of $x$ and $y$ will not exceed $100$.

Output Format

• Output a single line containing two integers, $O(x, y)$, representing the intersection point of $l_1$ and $l_2$.

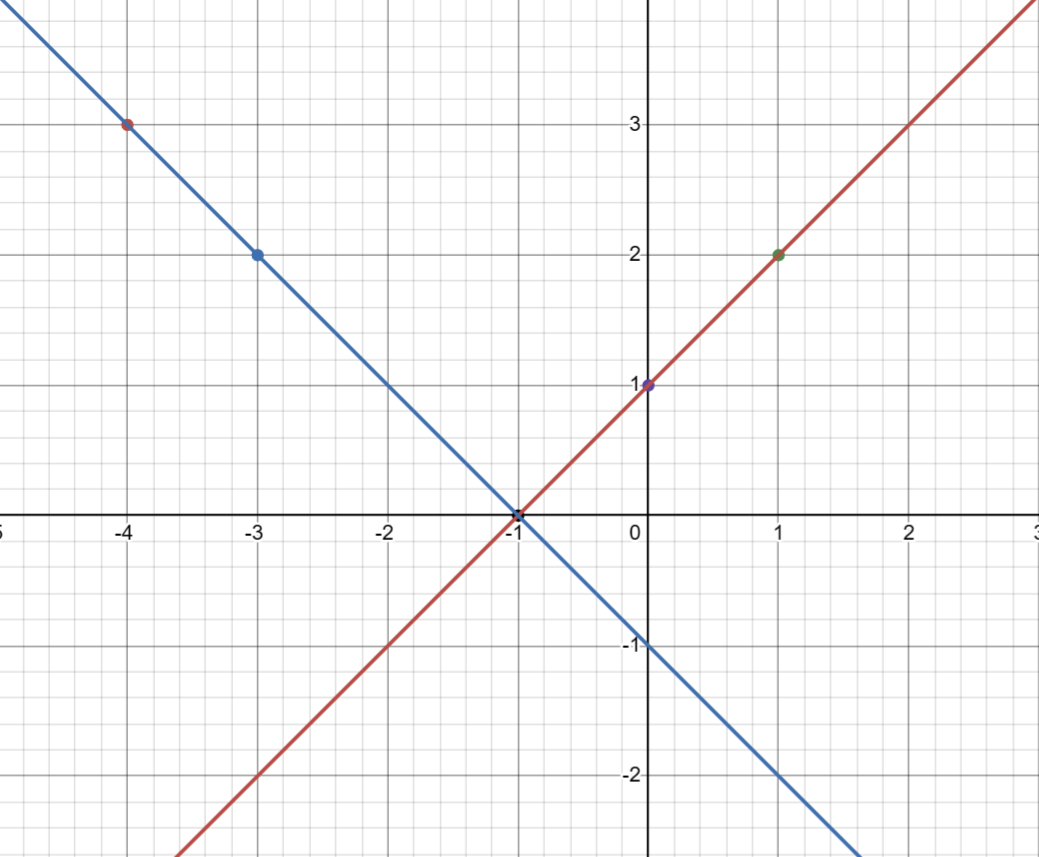
Sample #1

Sample Input #1

-4 3 -3 2
1 2 0 1

Sample Output #1

-1 0

Sample #2

Sample Input #2

2 3 1 2
-3 4 -2 3

Sample Output #2

0 1

Notes

For Sample #1, the intersection point of the two lines is illustrated as: